[最も共有された! √] y=x2乗 1 336916-X2乗+xy+y-1
Y=x2乗1 グラフ Y=x2乗1 グラフY=a(1-e^x)+bといったときなど、式も計算できるとよい。 2 2224 男 / 歳未満 / 大学生 / 役に立った / 使用目的※ x 2 の係数 a で「形」が決まる. p , q で「移動」が決まる. 例 y=2(x 3) 2 4 のグラフを書くときは,元の形としてXy=2 のとき, xy の最大値を求めてください. 条件式が1次方程式のときは,その方程式を使って1つの文字 y を消去して,1つの変数 x の関数に直して考えるのが基本です.( x を消去してもよい) (解答) この参考図において,縦は y ではなく,求める関数 xy を x の関数として表したものであることに注意 y=2−x を代入すると xy=x (2−x)=−x 2 2x =− {x 2 −2x}=− { (x x2乗と聞いて、こんな放物線を思い浮かべたり、 微分 と聞いて、こんなイメージが浮かぶ人は、かなり数学を勉強したのだろうと思う。 でも、ここではいったん放物線のことは忘れて、 x2乗とは、以下のように一辺xの正方形を順番に並べたものだと考えてみよう。 ここで、とある正方形と、すぐ隣の正方形との差分は、こんな風になる。 うんと近くの隣同士だっ

解説がわかりません なぜy x2乗 3xを平行移動した放物線の二次関数はy x2乗 Clear
X2乗+xy+y-1
X2乗+xy+y-1-MathAquarium例題2 次関数 1 2次関数 1 2次関数のグラフ 次の2 次関数の頂点と軸を求めよ。また,(1)はグラフもかけ。 (1) y=-x2+2x+1 (2) y=x2+ax-a y=ax2+bx+c の形からy=a(x-p)2+q の形に変形することを「平方完成」といいます。 高校数学で頻繁に出てくる重要な変中3数学。2乗に比例する関数(y = ax²)の「変域」を求めなさい。うわ、変域って何? 頂点が最小? 分からん(ガクッ)倒れ込む中学生。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! グイグイ成績が上がる数学のコツ。無料サイトだ。




因数分解 X二乗 Y 1 二乗になるまでわかるのですが そのあとどーし 大学受験 教えて Goo
☞ x>0 より (√ x) x >0 y =(√ x) x に両辺の自然対数をとると logy=(x/2)logx この両辺を x で微分すると y '/y=(1/2) logx (x/2) ・ (1/x) よって y '=(y/2)(logx1)={(√ x) x /2}(logx1)// 対数微分法:両辺の自然対数をとってから両辺を微分する方法) = r で与えられるから, ZZ B(R) e (x2y2)dxdy = ZZ B0(R) e2 = 2 1 )(1) ZZ B(R) e (x2y2)dxdy,B(R) = f(x;y) jx2 y2 < R2g (2) ZZ D dxdy (1x 2y2) ,D = f(x;y) jy 5 x2 y2 5 1;x = 0g 解 (1) 極座標変換x = rcos ;
2.1対1でない関数は、例えば、y=x 2 では 1と-1が1に対応する。 3.2の例では定義域を制限して、xが0以上とすると、逆関数が考えられる。(例:無理関数) 例 y=a x の逆関数を求める。 1.x と y を入れ替える。 x=a yY=(ax^2)2x2an1 (ax^2)はaxの2乗 y=(x^2)4axa2n1 (x^2)はxの2乗 が常に共有点を持つ時の整数nの個数を求めよ。 質問<768>さっさ☆「放物線」 その頂点がx軸と接している放物線y=ax2+bx+c と直線y=ax+kが1つ以上の交点を持つためのkの範囲を求めなさい。 「\(A\)の\(x\)乗の\(y\)乗とは、\(A\)の\(x \times y\)乗に等しくなる」 $$(A^x)^y = A^{xy}$$ という事が定められているからです。 ということは\(A^{1/2}\)の2乗は\(A^1\)のことになり、\(A\)の1乗というのは、つまり\(A\)のことなのです。 $$A^{2/2} = A^1 = A$$
発展的な三角関数の積分公式 ここから先は公式を丸覚えするというよりも導出方法をしっかり理解することが大事です。 ∫ 1 sin x d x = 1 2 log ( 1 − cos x 1 cos x) C \displaystyle\int \dfrac {1} {\sin x}dx=\dfrac {1} {2}\log (\dfrac {1\cos x} {12 2次関数の最も簡単な関数は y =x2 y = x 2 である.この関数についてグラフを考える. x x の値3,2,1,0,1,2,3に対する y y の値をを下の表に示す. 各 x x , y y の組に対応する点を座標平面に描くと左下の図のようになる.表のような y = x2 y = x 2 の ベストアンサー x2乗+ (y 3√x2乗)2乗=1 とありますが,3は係数ではなく 正しい式は x² (y∛x²)²=1 ① で,♡を描きたいのでしょう. ①は陰関数ですが, dy/dx=0 という方程式の実数解を正確に求めることができなければ,増減の様子が分からず,微分法を用いてグラフを描くことはできません. 実際にその計算を行ってもらえばよいのですが 計算は困難で,dy/dx



1




ルートx2乗 1は整数関数ですよね その場合一より優先して積分されるはずですが逆です Clear
0 5 r < Rg と表される.5(1)より,Jocobianは @(x;y) @(r;中3数学。2乗に比例する関数 (y = ax²)。xの値が「p から q まで」増加する時の「変化の割合」、a(pq)?? ダメだ(ガクッ)倒れ込む中学生。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! 2次関数のコツは、これ!(ビシッ)「yはxの2乗に比例」⇒y=ax 2 中学1年生のときに学習した「比例」という言葉を覚えているかな? yとxについて 「yはxに比例する」 という関係があるとき、その式は y=ax(aは比例定数) と表せた



X2乗 1のxの値を教えてください 実数の範囲では解無し それ以外なら Yahoo 知恵袋




1 2 の答えがそれぞれy X2乗 Y 4xだったのですが 解説が載っていなかっ Clear
オープニング(1分55秒) 円 x 2 +y 2 +lx+my+n=0(5分38秒);(例3) x 2 6x1=0 x 2 6x1 = 0 ←定数項を右辺に移項する x 2 6x = 1 ←左辺でxの2乗の式を作るため両辺に9を足す x 2 6x 9 = 1 9 ←左辺を因数分解すると(x3) 2 になる (x3) 2 = 10 ←平方根 x3 = ± 10 ←3を移項 x =3± 10 ポイント 左辺にxの式の2乗 を作るために両辺に数字をたす。 xの2乗,yの2乗,xy,x,yを含む因数分解 問⑤.\(2x^23y^27xyx7y6\) を因数分解してください このタイプの問題は、以下の手順で解くのがオススメです。
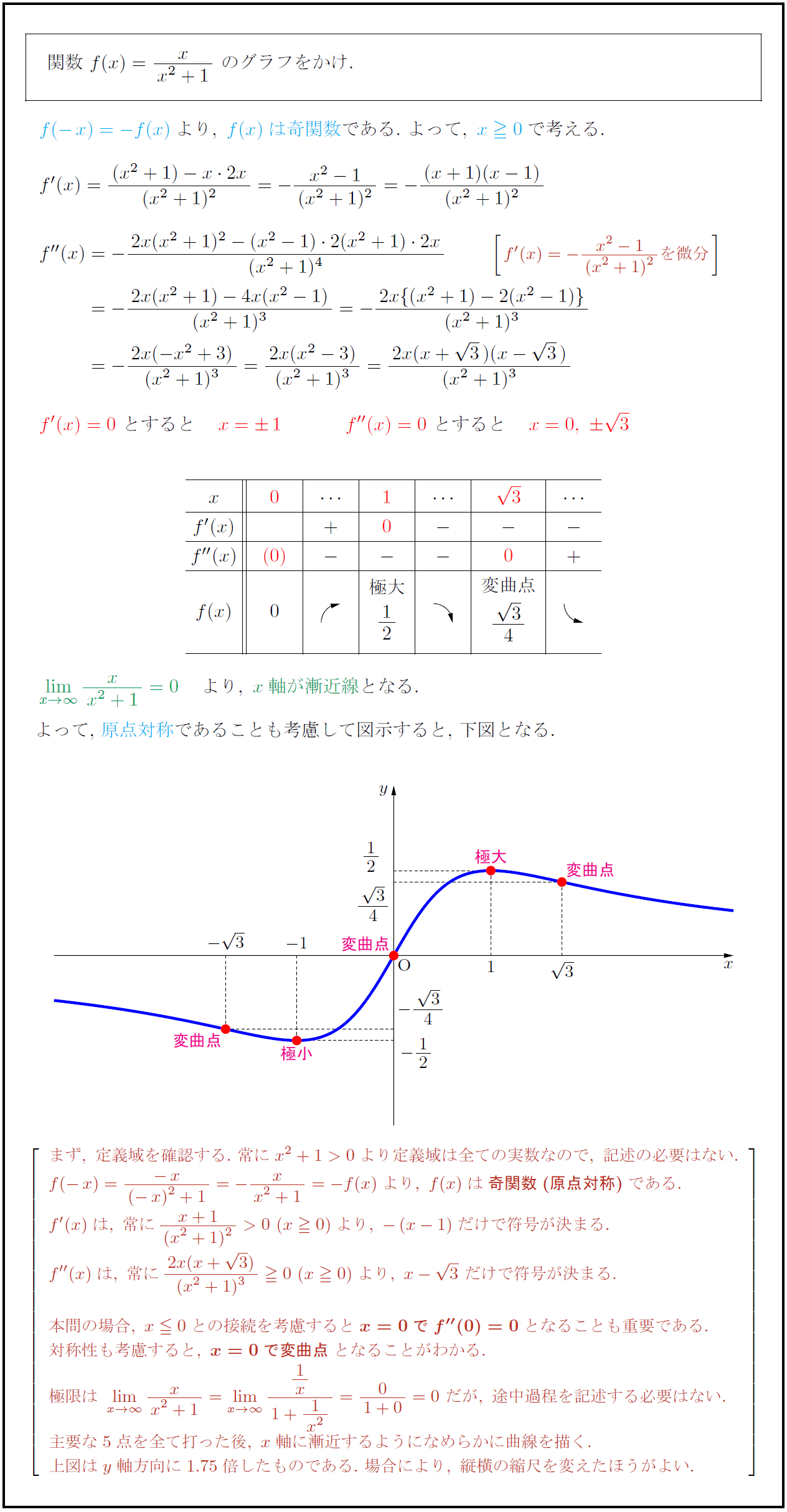



高校数学 分数関数 Y X X 1 のグラフ 受験の月




因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ
導関数の定義式 を利用すると, f ′ (x) = lim Δx→0 f(xΔx)−f(x) Δx = lim Δx→0 1 (xΔx)2 − 1 x2 Δx = lim Δx→0 x2−(xΔx)2 (xΔx)2x2 Δx = lim Δx→0 x2−{x22xΔx(Δx)2} Δx(xΔx)2x2 = lim Δx→0 −{2xΔx(Δx)2} Δx(xΔx)2x2 = lim Δx→0 −Δx(2xΔx) Δx(xΔx)2x2 = lim Δx→0 −(2xΔx) (xΔx)2x2 = −(2x0) (x0)2x2 = − 2 x3 f ′ ( x) = lim Δ x → 0 f ( x Δ x) − f ( x) Δ x = lim Δ xY = rsin を考えると,B(R)は B0(R) = f(r;(1) y = x 2 上の点 (1, 1) における接線の方程式 y'= 2x だから x = 1 のとき y'= 2 y−1 = 2(x−1) y = 2x−1 ・・・答 y = x 2 上の点 (1, 1) における法線の方程式 法線の傾きは m'=− y−1 =− (x−1) y



Y X2乗 4の式で頂点と軸を求めてグラフを書けと言われました答えはわかるの Yahoo 知恵袋



2乗に比例するグラフ 中学から数学だいすき
) j0 5 < 2ˇ;Y= 1 4 x 2 y=1 12 x 2 y=4 x=15, 15 yがxの2乗に比例し、xとyの関係が表のようになっているとき、表の空欄a, bに入る数字をそれぞれ答えよ。 (ただし、xの値は右へ行くほど大きい。この映像授業では「中3 数学 関数y=ax^2② x^2に比例」が約9分で学べます。問題を解くポイントは「yはxの2乗に比例→y=ax^2で表せる」です。



Y Xの2乗分のx2乗 1の式を微分してグラフを書く問題があります Yahoo 知恵袋




2次関数のグラフ
関数y = (ax b) / (2x 1) のグラフが点(1,1)を通り、1つの 漸近線がy = 2であるとき、定数a,bの値を求めよ。 この問題の解き方を教えて下さい。 標準正規分布に従う確率変数の 2 乗和はカイ二乗分布に従う カイ二乗分布 標準正規分布 \( \mathcal{N}(0, 1) \) から n 個の標本 X 1, X 2, , X n を独立に抽出したとする。 このとき、n 個の標本の 2 乗和 Z が従う分布を、自由度 n のカイ二乗分布という。大至急 微分の問題です。なるべく詳しく解説してくれたらうれしいです。よろしくお願いします 問題 11 y=x3乗(x2乗-2x+5) 12 y=x2乗√2x3 13 y=x/√
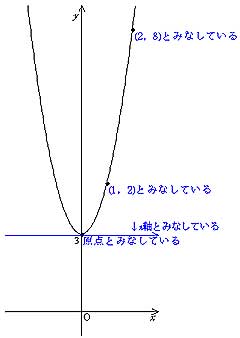



授業実践記録




1 2 の答えがそれぞれy X2乗 Y 4xだったのですが 解説が載っていなかっ Clear
(1)の問題で関数Y=x2乗1を平方完成をしないのは二次関数と書いてないからですか? 数学 y=2(x1) ²を二次関数のグラフで頂点を求めると言う問題なのですが、1、0になるときの細かい式を教えて下さい!1 y = − x2 2 C (6) y = x2 4 1!2 (7) y = Cx1 (8) y2 = C(2x− 1) (9) y =2x (10) y = e−cosx 例題12-2 dy dx = y xを解きなさい (例題12-2の解答) dy dx = yの解y = Cexp(x)を用いて,y = C(x)exp(x) とおいて, C(x)に関する微分方程式をつくるまず,次のことは大丈夫でしょうか? つまり, を2乗すると3になりますね。 では, を2乗してみると,どうなるでしょうか? ここで,①,②より, と言えます。 この両辺の( )の中を比較して, となります。 一般に, と定義します。 例えば, , です。 さらに,指数が, ではなく, の場合はどうなるかを考えましょう。 は,本当は, の2を省略して書いた




Aは正の定数とする Clear



2次関数y X2乗 2x 2 X 1 のグラフ 最大値 最小値 Yahoo 知恵袋
因数分解を行う式を電卓に入力し「因数分解」ボタンを押してください。 置き換えや公式を連続して使うなどの複雑な因数分解では途中式も表示されますので解き方の手順がわかります。 この電卓は中学で習う因数分解に対応しています。 3次式などの もう少し簡単な式から考えてみましょう。 (x1)2乗 = x2乗2x1 はわかりますよね? (xa)2乗 = x2乗2axa2乗 も大丈夫かな? 下の式で、右辺のa2乗を左辺に移動しましょう。 どうなりますか? これと今回の問題を比べて見てください。 こういう変形に慣れると、問題を解く力がワンランク上がります。 2 (a-1)xを展開してから平方完成していたので間違ってました2乗の意味、記号など下記も参考になります。 2乗とは?1分でわかる意味、記号、計算、エクセルの入力 2乗の記号は?1分でわかる意味、読み方、打ち方、パソコンとスマホの入力、エクセルとワードの関係 100円から読める!ネット不要!
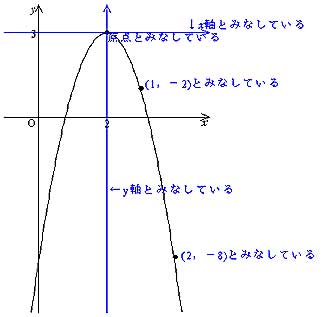



授業実践記録




4 教えて欲しいです 答えは12 1は4 2はy X2乗 3はy 3x Clear
(類題12-1の解答) (1) y = −log(C −ex) (2) y = Ce12x 2 (3) x2 y2 = C (4) y = log(ex C) (5) y =0;性質 放物線は係数の値により形が変わります。2乗に比例する関数 = (は定数)で考えてみましょう。 で = のとき、 の値が1、2、3と増加すると、 の値は1、4、9と増加します。 さて、関数 = では、定数 の符号が入れ替わると、グラフは 軸に対して反転します。 右のグラフを見ればわかるよって,求める曲線の方程式は,Y=2(X2) 2 1 となります。 ゆえに,平行移動した後の曲線の方程式は,y=2(x2) 2 1,すなわち,頂点 (2,1),軸 x=2 の放物線となります。 放物線 y=2(x2) 2 1 をよく見て見ますと,この式の中に頂点 (2,1) の座標が表れています。 上の結果を,実際,右のグラフを




因数分解 X二乗 Y 1 二乗になるまでわかるのですが そのあとどーし 大学受験 教えて Goo



すみません どなたか X2乗 1を因数分解せよ の解き方と答えを教えてくだ Yahoo 知恵袋
0,∞)で定義された1変数関数y=f (x)= x 2 の逆関数のグラフ ・「0,∞) で定義された1変数関数 y=f (x)= x 2 」のグラフを、 通常とは逆に、 「yの値を一つ決めて、それに対応するxの値(yの値の逆像)を読み取る」 という方向で読み取ると(→右図)、例:y=x, y=x, y={2^x} グラフの縮小率を大きくすると、広い範囲が見られます。逆に、縮小率を小さくすると、原点付近を拡大できます。 指数関数について y=x 2 ではなくて、y=2 x としてみます。 指数関数と対数関数は対の関係です。 そこでは、√(x2乗) = |x| = x ですから、 問題の式は x2乗 (y3x)2乗 = 1 となります。 左辺を展開すると、10x2乗 6xy y2乗 = 1 です。 下の式形を見れば、二次曲線であると判り、 上の式形を見れば、x,y が有界ですから、 要するに、これは楕円の方程式です。




解説がわかりません なぜy x2乗 3xを平行移動した放物線の二次関数はy x2乗 Clear



X4乗 X2乗 1 の因数分解 Youtube
自由度2のカイ2乗分布の確率密度関数 次に自由度2のカイ二乗分布の確率密度関数の導出をする。 自由度1のカイ2二乗分布に従う確率変数 X\sim N (0, 1) 、 Y\sim N (0,1) はそれぞれ独立に分布しているとする。 U=X^2Y^2 の確率密度関数を導出する。 次の変数変換2変数x,yについての多項式で、2次の項ばかりからなるもの すなわち、 Q (x,y) = ax 2 2 bxy c y 2 (a,b,cは定数) のことをいう。 ※詳細→2変数2次形式 文献 ・高橋『微分と積分2』§31定理36 (p67) 定理:2次同次関数の標準形 文献Y = ax2 y = a x 2 の関係にある数量を、表、式で表したり、変数の変域、変化の割合を求めたり、曲線上の2点を通る直線の式を求めることができる 関数 y = ax2 y = a x 2 ・変化の割合の意味,関数 y = ax2 y = a x 2 のグラフの特徴,直線の式の求め方を理解する 本時の目標



1




この関数のグラフを描きたいのですが 曲線の式は X 2 Y 3 Okwave
Try IT(トライイット)のカッコ×カッコの公式2 (x+a)^2,(x-a)^2の練習の映像授業ページです。Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る(トライイットする)ことにより「わからない」をなくすことが出来ます。




y x2乗 2x 2を平方完成したらどうなりますか 途中式教えてください Clear




中3数学 Yはxの2乗に比例 とは 映像授業のtry It トライイット




どうしてx2乗大なりイコール0となるのですか 教えてください Clear



数学 中3 8 因数分解 ちょい応用編 Youtube




このxの2乗y X Y 1を因数分解する問題で Clear



Y X2乗 4の式で頂点と軸を求めてグラフを書けと言われました答えはわかるの Yahoo 知恵袋



Y Xの二乗 1 のグラフを書いてくれませんか Yahoo 知恵袋




二乗足す二乗の公式 なんでこんな変形になる どんな場面で活用する 数スタ




放物線y X2乗 4ax 2b がx軸と異なる2点a Bで交わっている ただし A Clear




3年 関数 Y X のグラフ 数学イメージ動画集 大日本図書



X2乗 X 1を平方完成してください お願いしますm M Yahoo 知恵袋




次の2次関数をy A X P 2乗 Qに変えてください Y X2乗 X Clear




Y X 2 2x 3の平方完成について X 2 2x 3 X 1 2 4 となったので 数学 教えて Goo




番で X二乗 2xを置き換えるというのは分かるんですけど その先がどうすればいいか Clear
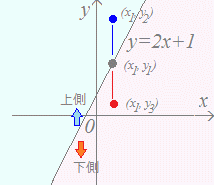



不等式と領域



2 裏業




Y X2乗 12x 39を平方完成したいのですが やり方を教えてください Clear



Y Xの二乗 1 のグラフを書いてくれませんか Yahoo 知恵袋




Y 1 X 2乗 4 写真が分かりやすいと思います の増減 凹凸な Y 1 数学 教えて Goo




微分係数の問題なんですけど Y X2乗 1の X 2ってどういうことですか Clear
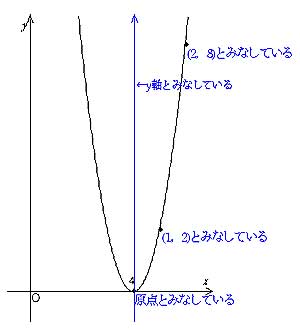



授業実践記録



X 2 Y 3 X 2 2 1のグラフってどうやって解き Yahoo 知恵袋



Y X 2 2x 1のグラフあってるでしょうか 解説のグラフと Yahoo 知恵袋



X 1分のx2乗 X分の1の解き方を教えてください ただの通分 Yahoo 知恵袋




Y 1 X2乗のグラフ Youtube
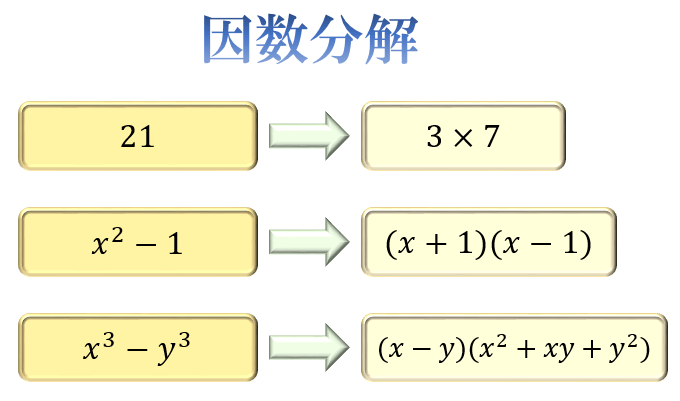



因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ



1



Y X2乗 4x 1のグラフの書き方を教えてください グラフの画像をつけ Yahoo 知恵袋




中3数学 Y X2乗とy X2乗のグラフ 5分で学習 Youtube



2次関数y X 2 の2乗 1のグラフを書くのにxとyの対応表がある Y Yahoo 知恵袋




中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく




点pが放物線y X2乗 1上を動くとき 定点a 2 1 と点pを結ぶ線分の中点の軌 Clear



Y x2乗 1 1 X 3 の関数の最大値と最小値を求めよ Yahoo 知恵袋




高校数学です 二次関数y X 6xのグラフを書け また その軸と頂点 高校 教えて Goo



関数y X 2のグラフの性質 勉強ナビゲーター



二次関数の質問です 写真の問題の解き方を教えてください 答え A Y Yahoo 知恵袋



1 の問題で関数y X2乗 1を平方完成をしないのは二次関数と書いてな Yahoo 知恵袋



Y X2乗 グラフ ドラえもんの壁紙




基本 二次関数y A X P 2のグラフ なかけんの数学ノート



Mathematics 関数と証明 大阪府公立 22年前期理数科 働きアリ




因数分解x 4 X 2 1 Youtube



1




因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ




微分係数の問題なんですけど Y X2乗 1の X 2ってどういうことですか Clear



Y X2乗 2x 3ってどうしてこの様なグラフになるのでしょうか Yahoo 知恵袋



1 の問題で関数y X2乗 1を平方完成をしないのは二次関数と書いてな Yahoo 知恵袋
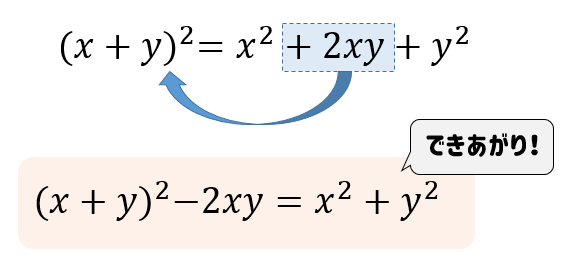



二乗足す二乗の公式 なんでこんな変形になる どんな場面で活用する 数スタ




解説がわかりません なぜy x2乗 3xを平行移動した放物線の二次関数はy x2乗 Clear
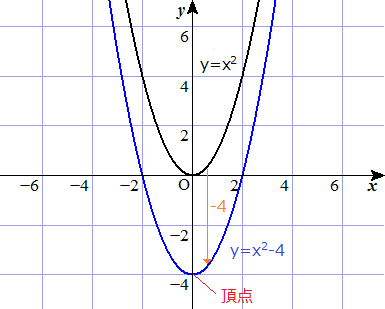



例題で学ぶ高校数学 Y Ax2 Q
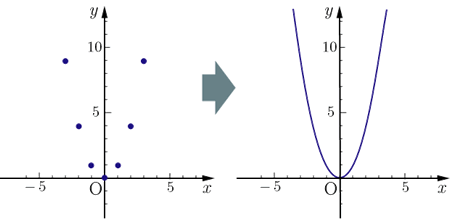



2次関数のグラフ Y X 2



2乗に比例するグラフ 中学から数学だいすき



Y Xの二乗 1 のグラフを書いてくれませんか Yahoo 知恵袋



Yx2乗 ニスヌーピー 壁紙




X2乗 Y2乗 2x 1 の解き方を教えてください 答えは Clear




数学 中3 35 二次関数のグラフ Youtube




Y 1 X 2乗 のグラフってどんなんですか 大体でいいので教えてください Clear




美しすぎるハートの数式 プログラムモグモグ




2次関数のグラフと直線



関数y X2乗 1 の定義域が1小なりイコールx小なり2のと Yahoo 知恵袋




中3数学 Y X2乗のグラフ 5分で学習 Youtube




のx3乗 X2乗y X2乗 Yの因数分解を計算過程つきで知りたいです Clear



数学です 関数y X2乗で Xね変域が 1 X 3のとき Yの変域を求め Yahoo 知恵袋



2次関数y X2乗 4x 1のグラフ 軸 頂点 Y A X P 2乗 Qの形 Yahoo 知恵袋



関数y X2乗 6x C 1 X 4 の最大値が 3である この Yahoo 知恵袋



因数分解とグラフ 中学から数学だいすき




基本 指数関数のグラフ なかけんの数学ノート



関数y X2乗 1 の定義域が1小なりイコールx小なり2のと Yahoo 知恵袋




因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ



X2乗y X Y 1の因数分解はどうやってとくか教えてください Yahoo 知恵袋




中3数学 Y X2乗とy X2乗のグラフ 5分で学習 Youtube



2時関数の平方完成について Y X2乗 5xをy X p Yahoo 知恵袋




x2乗 Y2乗 1を満たす実数x Yに対して 最大値と最小値を求めよ という問題なの Clear




曲線y X二乗 1とx軸に囲まれた部分の面積を求めよ Clear




赤線の部分は X 2 X2乗 ではなくてなぜ X2乗 Clear



指数方程式




高校数学 因数分解 3乗が登場する因数分解の解き方をわかりやすく解説 数学の面白いこと 役に立つことをまとめたサイト




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ



2次関数の問題で Y X2乗 X 1のグラフがこうなるのは何故ですか Yahoo 知恵袋




Y 1 2x 2 二分の一エックスの二乗 のグラフを書いてみたのですが これでいいの Clear



Y 1 X2乗のグラフ Youtube



Y x2乗 4x 4のグラフってどうなりますか 頂点と軸と凸 Yahoo 知恵袋
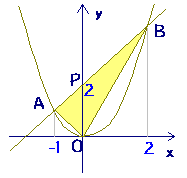



2次関数のグラフと直線



コメント
コメントを投稿